Cách giải bất phương trình bậc 2 và bài tập áp dụng

Trong toán học, bất phương trình bậc 2 là một dạng toán quen thuộc với các em học sinh. Tuy nhiên để giải được bài tập dạng này cũng không hề dễ dàng. Dưới đây là kiến thức cơ bản và công thức giải bài tập bất phương trình bậc 2 mà các em học sinh cần phải nắm rõ nhé.

1. Bất phương trình bậc hai

Bất phương trình bậc hai ẩn x có dạng ax2 + bx + c < 0 ( a#0)

Ví dụ dễ hình dung: x2 – 2 >0; 2x2 +3x – 5 <0;

Phương pháp giải bất phương trình bậc hai ax2 + bx + c < 0 có nghĩa là bạn đang tìm các khoảng mà trong đó f(x) = ax2 + bx + c  cùng dấu với hệ số a (trường hợp a<0) hoặc trái dấu với hệ số a (trường hợp a>0).

2. Dấu của tam thức bậc hai

Nhận xét: 

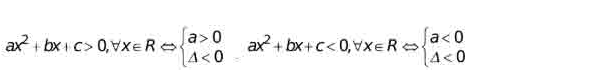
* Định lý: Cho hàm thức f(x) = ax2 + bx + c, Δ = b2 – 4ac.

– Nếu Δ<0 thì hàm thức f(x) luôn cùng dấu với hệ số a khi mà mọi x ∈ R.

– Nếu Δ=0 thì hàm thức f(x) luôn cùng dấu với hệ số a trừ khi x =-b/2a.

– Nếu Δ>0 thì hàm thức f(x) luôn cùng dấu với hệ số a trường hợp x < x1 hoặc x > x2 ; và trái dấu với hệ số a trường hợp x1 < x < x2 trong đó x1< x2 và x1; x2 đều là hai nghiệm của f(x).

Xem thêm Cách giải phương trình bậc 4 và các bài tập vận dụng

3. Cách xét dấu của tam thức bậc 2

– Trước tiên bạn hãy tìm nghiệm của tam thức

– Sau đó hãy lập bảng xét dấu dựa vào dấu của hệ số a

– Dựa vào bảng xét dấu và kết luận

4. Giải bất phương trình bậc 2

– Cách giải bất phương trình bậc hai ax2 + bx + c < 0 có nghĩa là bạn đang tìm các khoảng trong đó f(x) = ax2 + bx + c cùng dấu với hệ số a khi mà a<0 hoặc trái dấu với hệ số a khi a>0.

Theo đó, để giải bất phương trình bậc 2 thì bạn hãy áp dụng định lí về dấu của tam thức bậc hai.

5. Một số dạng toán thường gặp

Dạng 1: Giải bất phương trình bậc hai.

Phương pháp:

- Bước 1: Trước tiên, bạn hãy biến đổi bất phương trình về một vế là tam thức bậc hai và một vế bằng 0.

- Bước 2: Bạn hãy xét dấu vế trái của tam thức bậc hai và tìm ra nghiệm của phương trình.

Dạng 2: Giải bất phương trình tích.

Phương pháp:

- Bước 1: Trước tiên, bạn hãy biến đổi bất phương trình về dạng tích các nhị thức bậc nhất với tam thức bậc hai.

- Bước 2: Xét dấu nhị thức bậc nhất và tam thức bậc hai ở trên và tìm ra nghiệm phương trình.

Dạng 3: Giải bất phương trình chứa ẩn ở mẫu

Phương pháp:

- Bước 1: Trước tiên, bạn hãy biến đổi bất phương trình đã cho về dạng tích, thương đối với nhị thức bậc nhất và tam thức bậc hai.

- Bước 2: Xét dấu các nhị thức bậc nhất và tam thức bậc hai ở trên và đưa ra kết luận nghiệm.

Chú ý: Cần chú ý tìm điều kiện xác định với bất phương trình.

Dạng 4: Tìm điều kiện của tham số để bất phương trình vô nghiệm – có nghiệm – nghiệm đúng

Phương pháp:

Áp dụng một số tính chất:

- Trường hợp Δ<0 thì tam thức bậc hai cùng dấu với a.

- Căn bậc 2, bình phương và giá trị tuyệt đối của một biểu thức luôn không âm.

Dạng 5: Giải hệ bất phương trình bậc hai

Phương pháp:

- Bước 1: Giải từng bất phương trình có trong hệ.

- Bước 2: Kết hợp nghiệm và kết luận.

6. Các dạng bài tập bất phương trình bậc 2

Bài 1: Tìm m để bất phương trình x2 - 2(m + 1) + m2 + 2m ≤ 0 có nghiệm với mọi x ∈ [0; 1]

Hướng dẫn giải:

Đặt x2 - 2(m + 1) + m2 + 2m ≤ 0

Vậy bất phương trình có nghiệm đúng với ∀x ∈ [0; 1]

Phương trình f(x) = 0  có hai nghiệm thỏa mãn:

Vậy với -1 ≤ m ≤ 0 thỏa mãn điều kiện đề bài cho.

Bài 2: Tìm m để bất phương trình sau (m + 2)x2 - 2mx + m2 + 2m ≤ 0 có nghiệm.

Hướng dẫn giải

Xét 3 trường hợp:

- Trường hợp 1: Với m + 2 = 0 ⇒ m = -2 ta được:

(1) ⇔ 4x + 4 <0 ⇔ x < -1

Bất phương trình vô nghiệm

- Trường hợp 2: Với m < -2

Bất phương trình đã cho cũng có nghiệm

- Trường hợp 3: m + 2 > 0 ⇒ m > -2. Khi đó bất phương trình đã cho có nghiệm thì vế trái phải có 2 nghiệm phân biệt :

m > √2 và -2 < m < -√2

Vậy với |m| < √2 thì bất phương trình có nghiệm.

Bài 3: Tìm m để bất phương trình sau có nghiệm: m2x + 3 <  mx + 4

Hướng dẫn giải:

Bất phương trình tương đương với: m2x - mx < 4 ⇔ (m2 - m)x < 1; m2 - m = 0 ⇔m = {0;1} thì bất phương trình trở thành 0 < 1 đúng với mọi x .

Nên bất phương trình có vô số nghiệm.

Vậy bất phương trình có nghiệm với mọi giá trị thực của m.

Bài 4: Tìm tham số m để bất phương trình: f(x) = (m2 + 1)x2 + (2m - 1)x - 5 < 0

Nghiệm đúng với mọi x thuộc khoảng ( -1; 1)

Hướng dẫn giải:

Ta có:

Vậy để bất phương trình có nghiệm đúng với mọi x thuộc khoảng ( -1, 1) thì m ∈ (-1; √6 - 1)

Nguồn tổng hợp: Cao đẳng Y Khoa Phạm Ngọc Thạch