Công thức tính diện tích, chu vi hình thang và bài tập áp dụng

Hình thang là một trong tứ giác thường gặp trong hình học, việc nắm chắc được phần lý thuyết tính chu vi, diện tích hình thang giúp bạn dễ dàng áp dụng trong việc giải bài tập. Hãy tìm hiểu chi tiết trong bài viết trường Cao đẳng Y Khoa Phạm Ngọc Thạch tổng hợp dưới đây nhé. 

1. Tổng quan về hình thang

Hình thang là một tứ giác lồi gồm 2 cạnh song song mà rất dễ gặp trong cuộc sống hằng ngày. Hai cạnh song song này của hình thang sẽ được gọi là cạnh đáy còn những cạnh còn lại là cạnh bên. Cách tính chu vi hình thang khá đơn giản, bạn chỉ cần cộng tổng 4 cạnh còn công thức tính diện tích hình thang lại khó ghi nhớ hơn một chút.

Dưới đây là 3 loại hình thang thường gặp là:

• Hình thang thường
• Hình thang vuông
• Hình thang cân

2. Công thức tính diện tích hình thang

2.1. Cách tính diện tích hình thang thường

Cho hình thang ABCD với độ dài đáy AB là a, đáy CD là b và chiều cao h.

Công thức chung tính diện tích hình thang: chiều cao giữa 2 cạnh đáy nhân với trung bình cộng 2 cạnh đáy nhân.

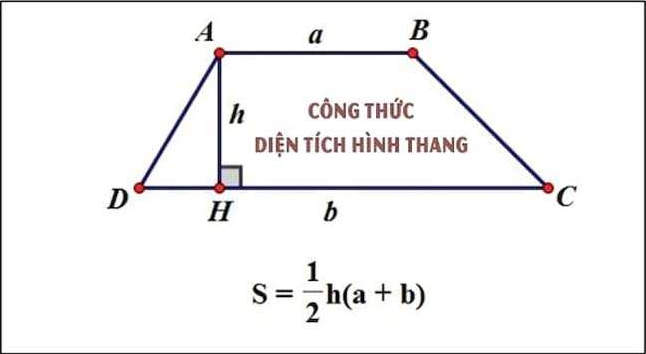
Trong đó:

• S là diện tích hình thang.
• a và b là độ dài 2 cạnh đáy.
• h là chiều cao hạ từ cạnh đáy a xuống b hoặc ngược lại (khoảng cách giữa 2 cạnh đáy).

Cách học thuộc cách tính diện tích của hình thang qua bài thơ dưới đây:

Muốn tính diện tích hình thang

Đáy lớn đáy nhỏ ta đem cộng vào

Cộng vào nhân với chiều cao

Chia đôi lấy nửa thế nào cũng ra

Ví dụ:

Một hình thang ABCD với chiều cao = 6cm, đáy bé a = 5cm, đáy lớn b = 9cm. Diện tích hình thang ABCD như thế nào?

Áp dụng công thức S = h x ((a +b)/2) = 6 x ((5+9)/2)= 42 (cm).

2.2. Công thức tính diện tích hình thang vuông

Theo ban tư vấn tuyển sinh của trường Cao đẳng Y Khoa Phạm Ngọc Thạch, hình thang vuông là một trường hợp đặc biệt của hình thang thường và có một góc vuông. Cạnh bên vuông góc với hai đáy, được gọi là chiều cao h của hình thang.

Công thức tính diện tích hình thang vuông tương tự như hình thang thường như sau: trung bình cộng 2 cạnh đáy nhân nhân với chiều cao giữa 2 đáy ( trường hợp này, chiều cao 2 đáy chính là ở đây chính là cạnh bên vuông góc với cả 2 đáy).

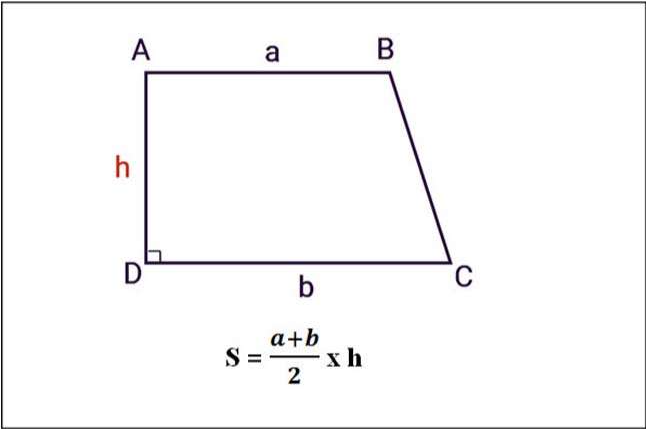
Trong đó:

• S là diện tích hình thang.
• a và b là độ dài 2 cạnh đáy.
• h là độ dài cạnh bên vuông góc với 2 đáy.

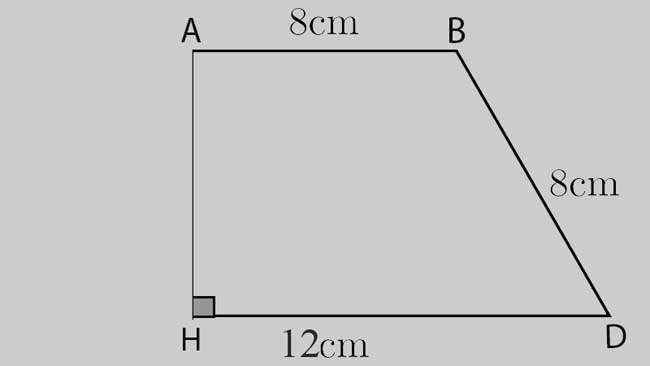
Cho hình thang vuông ABHD với độ dài đáy bé là 6cm và đáy lớn là 8cm. Trong đó, có cạnh bên AH = 8cm. Muốn tính diện tích hình thang trên thì làm như thế nào?

Áp dụng công thức diện tích hình thang vuông, ta có: S = h x ((a + b)/2) = 8 x ((6 + 8)/ 2) = 56cm.

2.3. Cách tính diện tích hình thang cân

Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. Trong đó 2 cạnh bên của hình thang cân sẽ bằng nhau và không song song với nhau.

Bên cạnh công thức tính diện tích của hình thang bình thường thì bạn có thể chia nhỏ hình thang cân để tính thành từng phần diện tích rồi cộng lại với nhau.

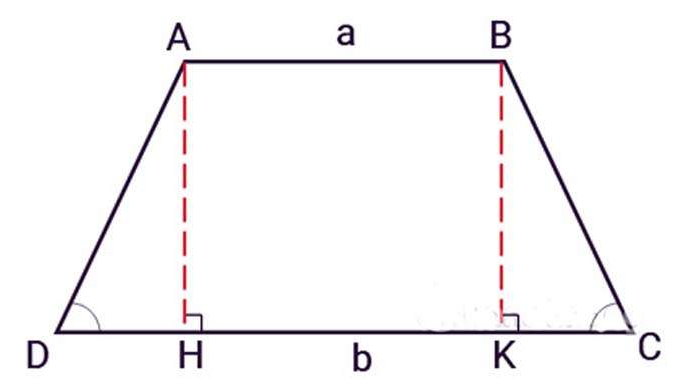
Ví dụ: Cho hình thang cân ABCD với 2 cạnh bên AD và BC bằng nhau. Đường cao AH và BE, hình thang sẽ được chia ra thành 1 hình chữ nhật ABEH và 2 hình tam giác là ADH và BCE. Áp dụng công thức tính diện tích hình chữ nhật cho ABHE và diện tích tam giác cho ADH và BCE sau đó cộng tất cả diện tích để tìm diện tích hình thang ABCD.

Cụ thể ví dụ:

Cho hình thang cân ABCD với chiều dài 2 cạnh bên AC và BD cùng bằng 7cm, cạnh đáy nhỏ bằng 8 cm và cạnh đáy lớn bằng 16 cm. Tính diện tích hình thang ABCD như thế nào?

Bài giải:

Dựa vào công thức tính diện tích hình thang, ta có S = h x ((a + b)/2) = 8 x ((16+8)/2) = 96cm.

Dựa vào công thức tính diện tích hình chữ nhật và công thức hình tam giác, ta có:

Gọi hai chiều cao của hình thang ABCD là AH và BE

=>S = 2 x S.ACH + S.ABEH = 2 x 1/2 x 4 x 8 + 8 x 8 = 56cm.

2.3.1. Tính độ dài cạnh đáy hình thang

Biết diện tích, chiều cao với độ dài của 1 cạnh đáy, thì bạn có thể tính được chiều dài một cạnh còn lại theo công thức sau:

AB= 2 x (SABCD/h) - CD

2.3.2. Tính diện tích hình thang khi biết 4 cạnh

Diện tích hình thang công thức dưới đây:

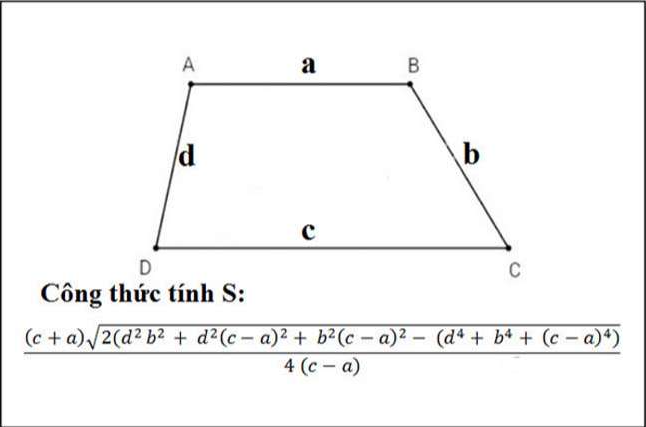
Trong đó:

+ a,c: lần lượt là độ dài 2 cạnh đáy.

+ b,d: lần lượt là độ dài 2 cạnh bên.

Trường hợp bài toán chỉ đưa ra câu hỏi tính diện tích hình thang khi cho biết thông số của 4 cạnh thường sẽ không có đáp án chính xác. Bởi bài toán này sẽ xảy ra rất nhiều trường hợp và ra kết quả diện tích cũng khác nhau. Dưới đây là ví dụ hình thang có 4 cạnh 4cm, 5cm, 6cm, 9cm được vẽ thành 3 hình khác nhau sẽ có diện tích khác nhau.

Trường hợp bài toán cho thêm dữ kiện về độ dài 4 cạnh nhưng chỉ rõ đó là cạnh nào thì bạn có thể tính chính xác được diện tích hình thang. Chẳng hạn như khi bạn biết những cạnh đáy Q P, gồm cạnh đáy P dài hơn và 2 cạnh bên R và S.

Áp dụng công thức tính diện tích hình thang, bạn có thể tính như sau:

Ngoài trường hợp tính diện tích hình thang khi biết các cạnh thì bạn hãy tách ra 2 tam giác và 1 hình chữ nhật hoặc kẻ thêm đường giao giữa 2 cạnh bên. Sau đó hãy áp dụng công thức Heron tính diện tích tam giác, từ đó suy ra được diện tích hình thang. Đây là cách áp dụng trong giải bài tập ở trên.

2.3.3. Công thức heron tính diện tích tam giác

Gọi S là diện tích và độ dài 3 cạnh tam giác lần lượt là a, b và c

3. Công thức tính chu vi hình thang

3.1. Tính chu vi hình thang

Hình thang là tứ giác gồm hai cạnh đáy song song với tổng số đo các góc là 360 độ.

Công thức tính chu vi hình thang tính bằng tổng độ dài của 2 cạnh đáy với hai cạnh bên.

P = a + b + c + d

Trong đó:

P là ký hiệu chu vi.

a, b là hai cạnh đáy hình thang.

c, d là cạnh bên hình thang.

3.2. Công thức tính chu vi hình thang vuông

Cách tính chu vi hình thang vuông tương tự với cách hình hình thang thường ơt trên.

P = a + b + c + d

Trong đó:

P là ký hiệu chu vi.

a, b là hai cạnh đáy hình thang.

c, d là cạnh bên hình thang.

Tính chu vi hình thang vuông

3.3. Công thức tính chu vi hình thang cân

Công thức tính chu vi hình thang cân bằng 1 lần cạnh bên cộng với tổng 2 cạnh đáy:

P = (2 x a) + b + c

Trong đó:

P là ký hiệu chu vi.

a, b là hai cạnh đáy hình thang.

c, d là cạnh bên hình thang.

Xem thêm về:

Công thức tính chu vi và diện tích hình bình hành

Công thức tính chu vi và diện tích hình chữ nhật kèm thêm ví dụ

4. Lưu Ý Khi Giải Các Bài Tập Về Tính Chu Vi, Diện Tích Hình Thang

Trong quá trình giải toán, nhiều học sinh và bậc phụ huynh không biết “hình thang có thể tích hay không? Công thức tính thể tích hình thang cân thế nào?“. Với câu hỏi trên thì các bạn khó có thể tìm được đáp án trả lời bởi hình thang là đa giác trong hình học phẳng, và không có thể tích như hình không gian.

Với kiến thức hình học cấp 2, sẽ giúp bạn tiếp cận được nhiều dạng bài tập hình thang khác nhau. Tuy nhiên không chỉ đơn giản dừng lại cách tính chu vi, diện tích hình thang mà bạn sẽ phải tư duy sâu và kết hợp các tính chất góc (tổng 2 góc kề 1 đáy trong hình thang bằng 180°), tính chất đường trung bình của hình thang và các cạnh bên,… Tuy nhiên, với cấp tiểu học chỉ giúp các bạn nắm được công thức tính diện tích hình thang kể trên giúp giải được đa số các bài toán tại chương trình này.

Bài viết trên đây giúp bạn tìm hiểu về công thức tính diện tích, chu vi hình thang như thế nào? Đừng quên theo dõi bài viết tiếp theo để cập nhật kiến thức hữu ích. Chúc bạn thành công!