Việc nắm chắc công thức tính chu vi và diện tích hình thoi sẽ giúp bạn vận dụng dễ dàng trong giải bài tập. Ngoài ra còn có những bài tập vận dụng giúp các em trau dồi kiến thức toàn diện hơn. Hãy cùng tìm hiểu chi tiết bài viết dưới đây nhé.
1. Tính chất và dấu hiệu nhận biết hình thoi
– Giới thiệu
Theo ban tư vấn tuyển sinh Cao đẳng Y Khoa Phạm Ngọc Thạch, Hình thoi được biết là một tứ giác với 4 cạnh bằng nhau. Bên cạnh đó, hình bình hành có 2 cặp cạnh không gần kề nhau bằng nhau hoặc 2 đường chéo vuông góc với nhau thì sẽ thành hình thoi.
– Tính chất
+ Hình thoi có đầy đủ tính chất của hình bình hành, cụ thể là: Những cạnh đối song song và bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm mỗi đường.
+ Hai đường chéo của hình thoi sẽ vuông góc với nhau.
+ Hai đường chéo là các đường phân giác của các góc thuộc hình thoi.
– Dấu hiệu nhận biết
Để nhận biết được hình thoi, bạn cần phải căn cứ vào những đặc điểm sau:
+ Tứ giác gồm 4 cạnh bằng nhau.
+ Hình bình hành bao gồm 2 cạnh kề bằng nhau.
+ Hình bình hành sẽ có 2 đường chéo vuông góc với nhau.
+ Hình bình hành gồm 1 đường chéo được xem là đường phân giác của một góc.
2. Công thức tính diện tích hình thoi
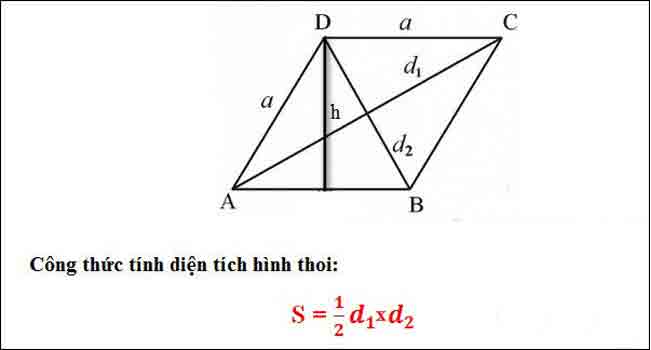
* Tính diện tích hình thoi dựa vào hai đường chéo
S=½ d1 x d2
Trong đó:
+ d1 : đường chéo thứ nhất
+ d2 : đường chéo thứ hai
Ví dụ 1: Cho biết một hình thoi ABCD đo có hai đường chéo cắt nhau lần lượt là d1 và d2 tương ứng 6 cm và 8 cm. Tính diện tích hình thoi ABCD bằng bao nhiêu?
Áp dụng công thức tính diện tích hình thoi, ta có d1 = 6 cm và d2 = 8 cm. Ta được kết quả như sau:
S = 1/2 x (d1 x d2) = 1/2 (6 x 8) = 1/2 x 48 = 24 cm2
Đáp số: 24cm2
* Tính diện tích hình thoi dựa vào cạnh đáy và chiều cao
Công thức là: S= h x a
Trong đó:
– h: Chiều cao của hình thoi
– a: Cạnh đáy
Ví dụ 1: Cho hình thoi ABCD với các cạnh AB = BC = CD = DA = 4 cm, còn chiều cao của hình thoi = 3cm. Tính diện tích của hình thoi ABCD bằng bao nhiêu?
Giải: Áp dụng theo công thức diện tích hình thoi ở trên thì ta có chiều cao h = 3cm, a = 4cm. Ta sẽ có kết quả dưới đây:
S = a x h = 3 x 4 = 12 cm2
Đáp số: 12cm2
Ví dụ 2: Cho hình thoi ABCD với cạnh đáy bằng 10 cm và chiều cao là 7 cm. Tính diện tích hình thoi ABCD bằng bao nhiêu?
Lời giải: Ta có cạnh đáy a = 10 cm và chiều cao h = 7 cm. Suy ra, diện tích hình thoi là: S = a.h = 10 x 7 = 70 cm2
* Tính diện tích hình thoi dựa vào hệ thức trong tam giác khi biết góc của hình thoi.
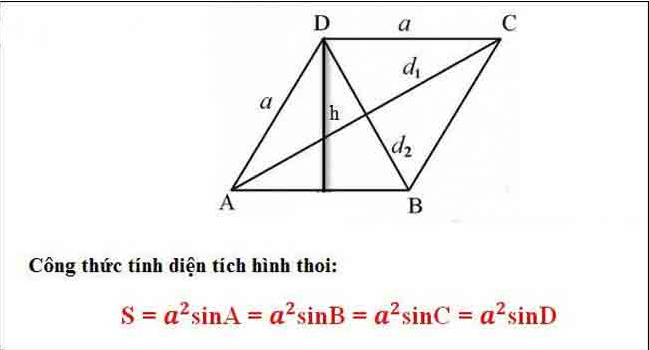
Trong đó: a: cạnh hình thoi
Ví dụ: Cho biết hình thoi ABCD với cạnh hình thoi = 4cm và góc A = 35 độ. Tìm diện tích hình thoi ABCD.
Giải: Áp dụng công thức tính diện tích hình thoi ở trên, ta có cạnh a = 4, góc A = 35 độ. Ta sẽ có kết quả dưới đây:
S = a2 x sinA = 42 x sin(35) = 9,176 (cm2)
3. Lưu ý khi tính diện tích hình thoi:
– Đơn vị diện tích hình thoi là m2, cm2 …
– Khi giải bài tập thì bạn hãy để ý đơn vị mà đề bài đưa ra có cùng nhau không. Nếu chưa thì bạn hãy đổi sang cùng một đơn vị trước khi làm.
Bài tập vận dụng: Tính diện tích hình thoi ABCD với cạnh dài 6cm và biết một trong các góc của nó với số đo là 60°.
Với những dữ liệu ở trên thì bạn vẫn chưa đủ để áp dụng tính diện tích hình thoi luôn. Với dạng bài này, bạn cần áp dụng tính chất tam giác đều, tính chất hình thoi và các cạnh trong tam giác vuông để tính được đường chéo của hình thoi. Dưới đây là các bước giải bài tập:
Bước 1: Vẽ hình và ghi chú những dữ kiện đã biết.
Bước 2: Vận dụng tính chất của hình thoi ta được:
Biết đường chéo AC là phân giác của góc A, do vậy góc DAC được tính bằng 1/2 góc DAB và bằng 60°. Các góc trong tứ giác có tổng bằng 180°. Bởi vậy mà tam giác ADC sẽ là tam giác đều với cạnh AC bằng 6cm. I là trung điểm AC => AI=3cm.
Bước 3: Tính độ dài DI
Tam giác DIA vuông tại I, suy ra độ dài cạnh DI tính như sau:
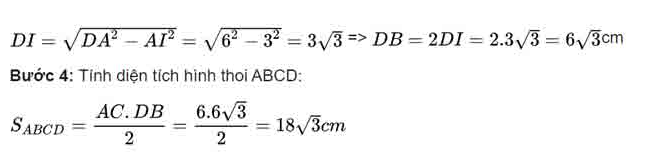
Ví dụ 3: Tính diện tích hình thoi ABCD khi biết chiều dài cạnh bên là 2cm với góc là 30 độ.
Lời giải:
Chiều dài của cạnh bên hình thoi: a = 2 cm
Góc A bằng 30 độ, suy ra góc C đối diện với góc A bằng 150 độ
Tính diện tích hình thoi ABCD bằng:
S= a². sin α S= 2². sin 30 = 2 cm2 S= 2². sin 150 = 2 cm2
– Giới thiệu:
Diện tích của hình thoi được tính bằng nửa tích hai đường chéo của hình thoi hay bằng tích của chiều cao với cạnh đáy tương ứng.
– Công thức:
S = ½ (d1 x d2)
S = h x a.
– Trong đó:
+ S: Diện tích hình thoi.
+ d1, d2: Lần lượt là kích thước 2 đường chéo của hình thoi.
+ h: Chiều cao hình thoi.
+ a: Độ dài cạnh đáy.
Ví dụ:
Tính diện tích hình thoi ABCD khi mà biết chiều dài của đường chéo lần lượt là d1 = 5cm, d2 = 10cm.
Giải:
S = ½ (d1 x d2) = ½ (5 x 10) = 25 cm2
4. Công thức tính chu vi hình thoi
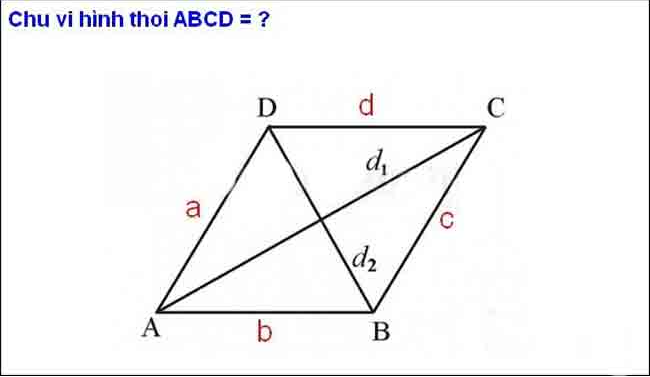
– Giới thiệu
Chu vi hình thoi gồm tổng độ dài 4 cạnh xung quanh của hình thoi.
– Công thức
Chu vi hình thoi được tính bằng tổng độ dài các cạnh cộng lại với nhau hay độ dài của một cạnh nhân với 4.
C = a x 4.
– Trong đó:
+ P: Chu vi hình thoi.
+ a: Độ dài một cạnh bất kỳ của hình thoi.
– Ví dụ:
Cho hình thoi ABCD khi biết chiều dài của một cạnh hình thoi là a = 5 cm.
Áp dụng công thức tính chu vi của hình thoi ở trên thì ta có: P = a x 4 = 5 x 4 = 20 cm.
– Ví dụ: Cho một hình thoi ABCD với độ dài các cạnh bằng nhau và bằng 7 cm. Tính chu vi của hình thoi bằng bao nhiêu?
Dựa vào công thức tính chu vi hình thoi ở trên thì ta có cạnh a = 7 cm. Ta có chu vi hình thoi ABCD sẽ được tính như sau:
P (ABCD) = a x 4 = 7 x 4 = 28 cm
5. Lưu ý khi tính diện tích, chu vi hình thoi
– Khi tính diện tích hình thoi, bạn hãy chú ý đến đơn vị của diện tích là đơn vị chiều dài + vuông. Chẳng hạn: cm2, m2,…
– Theo đó thì bạn hãy chú ý đến đơn vị đo chiều dài của hai đường cao và đường chéo với cạnh xem đã về cùng một đơn vị hay chưa. Hãy đưa về cùng một đơn vị đo rồi bắt đầu tính toán.
6. Công Thức Tính Đường Chéo Hình Thoi
Với công thức tính chu vi i, diện tích hình thoi ở trên, thì các bạn có thể áp dụng để tính được công thức tìm đường chéo hình thoi dưới đây:
* Tính đường chéo hình thoi khi biết độ dài của đường chéo và diện tích:
Khi biết diện tích hình thoi và độ dài của đường chéo (d1), thì các bạn có thể áp dụng để tính được 1 cạnh còn lại của hình thoi theo công thức sau: d2 = 2S/ d1
* Tính đường chéo hình thoi khi biết độ dài cạnh a, góc A bằng 60 độ
Vì ABCD là hình thoi nên các cạnh đều bằng a.
Xét tam giác ABC có: AB = BC = a
Lại có: ABC = 60 độ => Tam giác ABC là tam giác đều cạnh a.
=> AB = AC = BC = a
=> Độ dài đường chéo hình thoi có cạnh bằng A, góc A bằng 60 độ chính là AC = BD = a.
Thông tin trong bài viết trên đây giúp bạn tìm hiểu về công thức tính chu vi hình thoi và diện tích hình thoi như thế nào. Với bài tập áp dụng ở trên thì bạn có thể dễ dàng vận dụng trong những bài tập tiếp theo. Đừng quên theo dõi bài viết tiếp theo để cập nhật kiến thức liên quan nhé.





 Cách chọn khối thi Đại học phù hợp năng lực 2025
Cách chọn khối thi Đại học phù hợp năng lực 2025
 Top 10 Các Trường Cao đẳng Y Dược xét học bạ 2025
Top 10 Các Trường Cao đẳng Y Dược xét học bạ 2025
 Trường Cao đẳng Y khoa Phạm Ngọc Thạch có tốt không?
Trường Cao đẳng Y khoa Phạm Ngọc Thạch có tốt không?
 Nên học Điều dưỡng hay Hộ sinh để phát triển sự nghiệp?
Nên học Điều dưỡng hay Hộ sinh để phát triển sự nghiệp?
 Nên học Dược hay Điều dưỡng? Chọn ngành nào tốt hơn?
Nên học Dược hay Điều dưỡng? Chọn ngành nào tốt hơn?
 Ngành Tổ chức và Quản lý Y tế là gì? Ra trường làm gì?
Ngành Tổ chức và Quản lý Y tế là gì? Ra trường làm gì?

 Q. Tân Bình: Số
Q. Tân Bình: Số  Điện thoại: 0899 955 990 (Cô Nhung) | 0969 955 990 (Cô Huệ) | 0933519898 (Cô Yến) | 0961539898
Điện thoại: 0899 955 990 (Cô Nhung) | 0969 955 990 (Cô Huệ) | 0933519898 (Cô Yến) | 0961539898 Email:
Email: 



